— Я вчера у вас бракованные шарики купил…
— Что, сдуваются или лопаются?
— Нет, просто не радуют они меня…

Теория

Всем известна игра в жанре Match-3. Такой тип игр подразумевает объединение на поле шариков в комбинации из 3 или больше в ряд, после чего они лопаются добавляя очки в копилку. А если повезет, то исчезнувшие шарики повлекут за собой комбинацию исчезновений других шариков.

Обычно в таких играх также сверху добавляются новые шарики, забивая пустоты, но в данной задаче добавление новых шариков не будет, а сами шарики будут заменены на числа. Клетки с шариками имеют обозначения от 1 до 5, пустая - ноль.

Команды

Для создания алгоритма требуется использовать следующие фиксированные конструкции:

• get(<x>, <y>) - получение значения с поля по указанным координатам
• set(<x>, <y>, <value>) - изменить значение поля по указанным координатам (value от 0 до 5)
• size_x - ширина поля
• size_y - высота поля
• create(<name>[, <size>][, <structure>|<type>]) - создать переменную или переменную со структурой (array, list, stack, queue, dict, matrix), размер можно задать в произвольном формате
• stop(<results>) - завершает программу

< и > не относятся к программе, они показывают, что данная часть кода заменяется каким-либо именем или структурой. [...] означает необязательную структуру.

Получение данных и переменных производится в произвольном формате (в каком захотите). Циклы и тому подобные конструкции использовать либо из языков программирования, либо расписать свой формат (желательно использовать латиницу, можно расписать в БНФ). Если используете какую-то функцию, то распишите как она работает (в формате программы).

Команды могут быть изменены, например create можно опустить и рассматривать простое присвоение с указанием параметров, однако значительные отступления не возможны.

Пример алгоритма

Данный алгоритм лопает комбинацию внизу поля (если она возможна)

if (field(0, 0) == field(1, 0) == field(2, 0)) {
    pop(0, 0);
}

Если хотите чтобы ваш алгоритм был читаем: используйте отступы и разделители команд (например, точки с запятой)

Задача

Дано прямоугольное поле, размеры поля сохранены в константах size_x и size_y. Ось абсцисс идет слева направо. Ось ординат снизу вверх. Задачи решаются только последовательно. Если предыдущая задача не была решена хотя бы на половину, то остальное решение не засчитывается.

1 часть
Ваша задача проверить, можно ли сдвинуть шарик по указанным координате и направлению (для получения комбинации). Не забывайте учитывать границы поля и размеры возможной комбинации. На вход подается позиция и направление: 0 4 up, 10 29 right и т.п.

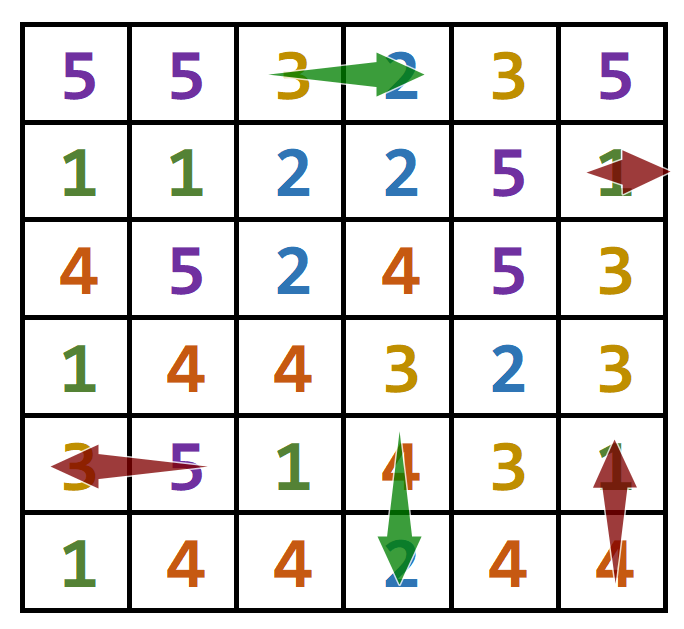
После выполнения будет доступна команда: move(<x>, <y>, <dir>) - сдвинуть шарик на поле (если это возможно), указав направление (up, down, left, right), используется не только для создания групп шариков, но и для смещения после изменения поля (учет физики падения)

2 часть
Требуется сделать проверку на то, можно ли лопнуть шарик, а если можно, то лопнуть все шарики в комбинации. Передвигать шарики не нужно. Это решение задает автоматическое уничтожение всех комбинации на указанной клетке в дальнейшем.

После выполнения будет доступна команда: pop(<x>, <y>) - лопнуть шарик на поле (если это возможно), если лопнуть один шарик, то группа шариков лопнется вместе с ним

3 часть
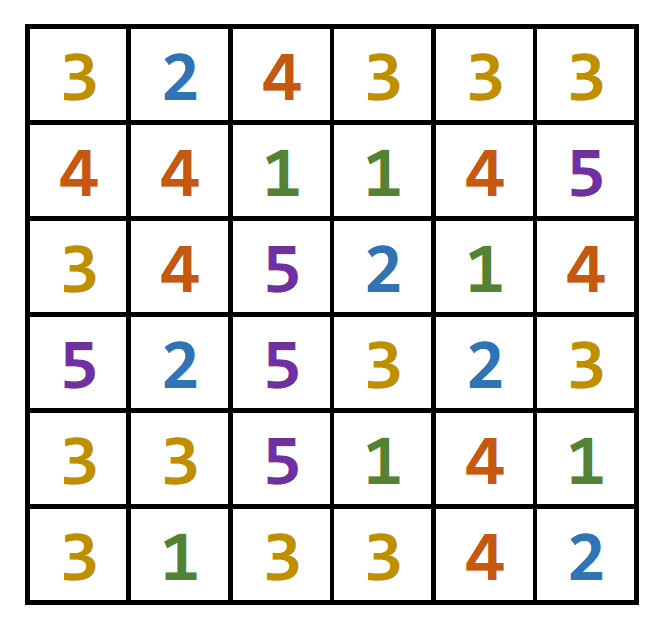
На поле забыли лопнуться несколько комбинаций, лопните их всех. Падение шариков не учитывать. Передвигать шарики не нужно. Лопнуть нужно только один шарик в комбинации, остальные лопнутся сами (так как это было сделано в прошлой задаче).

4 часть
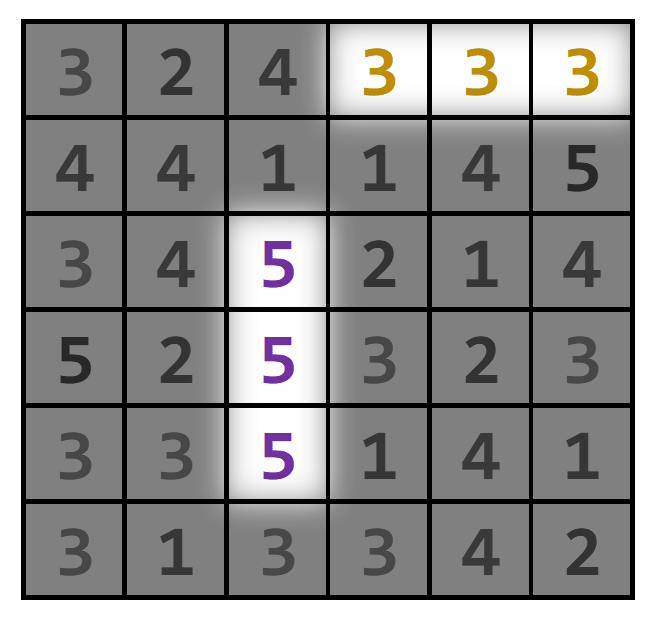
Найти максимальную комбинацию из шариков, которую можно составить передвинув один шарик. Укажите координату и направление сдвига в ответе, а также результат в очках (количество убранных шариков).

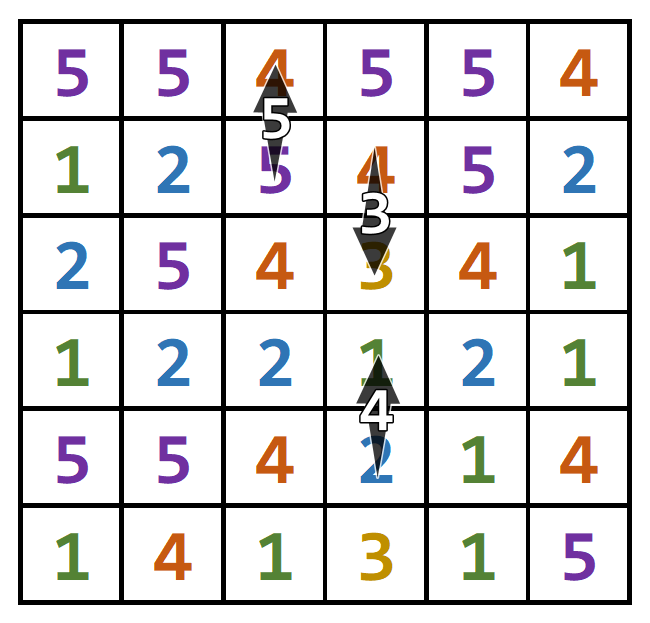
Ответ в примере: (2, 4, “up”), 5 очков

5 часть
Теперь добавим физику. Найдите максимальную комбинацию из лопающихся комбинаций, которые возникают после лопанья первой комбинации. Укажите координату и направление сдвига в ответе, а также результат в очках (количество убранных шариков). Новые комбинации лопаться автоматически не будут.

Ответ в примере: (1, 0, “up”), 13 очков

Ответ в примере: (3, 1, “down”), 19 очков

Комбинации смещений и координат могут быть разными (так как можно сдвинуть не саму клетку, а её соседа и получить тот же результат).

Что происходит в задачах?

Вашей задачей является симуляция игры, а точнее одного хода. Вы должны максимизировать прирост очков, не рассматривая дальнейшей выгоды. Каждая часть оценивается по-разному.

На Главную